Basics

Case study: Alarm State Machine

Building the machine

Binary encoded state value

As we have three states, we need here only two flipflops - this configuration will allows up to four states (00, 01, 10, 11).

We have to do some more calculation.

First, we have to decide how the states will be coded.
The sleep (1) state will be coded "00" as it is the switch on value and then there would be no need for a reset button to force this value.
The two other states lead to actions (switch on the "arm" indicator and switch on the alarm and the timer).
It will be much more easy to use for these two states the "01" and "10" as each of the fliflops output can be directly used to control the respective actions with no further logic

Hence, the state encoding:

The state AB=11 is not used and must not occur.

So the previous truth table

becomes:

Hence the equation for the two flipflops A and B:

with the following state number equations:

1 = A.B
2 = A.B
3 = A.B

We have then the equations with the A and B values only:

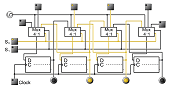
Which gives the following circuit:

This design method can be use for other state machines.